Umfang: Unterschied zwischen den Versionen
Aus Wiki.sah
E.T. (Diskussion | Beiträge) (ads) |
E.T. (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Der '''Umfang''' eines zweidimensionalen Objekts wird durch die Länge seiner Begrenzungslinie definiert. | Der '''Umfang''' eines zweidimensionalen Objekts wird durch die Länge seiner Begrenzungslinie definiert. | ||
== Kreis == | == Kreis == | ||
http://www.science-at-home. | http://www.science-at-home.de/bilder/wikidata/mathematik/kreis.gif | ||
{{Formel|='''U''' = d·π}} | {{Formel|='''U''' = d·π}} | ||
<br> | <br> | ||
| Zeile 20: | Zeile 12: | ||
== Ellipse == | == Ellipse == | ||
http://www.science-at-home. | http://www.science-at-home.de/bilder/wikidata/mathematik/ellipse.gif | ||
{{Formel|='''U''' ≈ π · (D + d) / 2}} | {{Formel|='''U''' ≈ π · (D + d) / 2}} | ||
<br> | <br> | ||
| Zeile 28: | Zeile 20: | ||
*[[Formeln Kreis]] | *[[Formeln Kreis]] | ||
{{Adsense responsive}} | |||
== Rechteck == | == Rechteck == | ||
http://www.science-at-home. | http://www.science-at-home.de/bilder/wikidata/mathematik/rechteck.gif | ||
{{Formel|='''U''' = 2·l + 2·b = 2·(l + b)}} | {{Formel|='''U''' = 2·l + 2·b = 2·(l + b)}} | ||
| Zeile 52: | Zeile 44: | ||
[[Kategorie:Mathematik]] | [[Kategorie:Mathematik]] | ||
[[Kategorie:Geometrie]] | [[Kategorie:Geometrie]] | ||
[[Kategorie: | [[Kategorie:Formel Geometrie]] | ||
[[Kategorie:Ad man]] | [[Kategorie:Ad man]] | ||
Aktuelle Version vom 12. Februar 2024, 09:45 Uhr
Der Umfang eines zweidimensionalen Objekts wird durch die Länge seiner Begrenzungslinie definiert.
Kreis
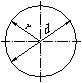
| U = d·π |
| U = 2π·r |
Faustregel für Kreisumfang
| U = 22/7 · d |
Ellipse
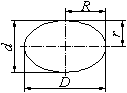
| U ≈ π · (D + d) / 2 |
| U ≈ π · (R + r) |
Siehe auch
Rechteck

| U = 2·l + 2·b = 2·(l + b) |
Siehe auch
Vieleck
| Der Umfang eines Vielecks ist die Summe seiner Seitenlängen |
Kreis/Ellipse U = Umfang r = Radius des Kreises d = Durchmesser des Kreises π = Kreiszahl Pi Rechteck l/b = Seitenlängen