Formeln Kreis: Unterschied zwischen den Versionen

Aus Wiki.sah
Zur Navigation springenZur Suche springen
(+linkblock)
(2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
__TOC__
 +
 +
{{Adsense linkblock 160x90}}
 +
 
== Kreis ==
 
== Kreis ==
  
−
http://www.science-at-home.net/bilder/wikidata/mathematik/kreis.gif
+
http://www.science-at-home.de/bilder/wikidata/mathematik/kreis.gif
  
 
{| style="text-align: right" border = "0" style="border-collapse: collapse" cellpadding="5" align="right"
 
{| style="text-align: right" border = "0" style="border-collapse: collapse" cellpadding="5" align="right"
Zeile 78: Zeile 82:
 
  ! style="text-align: left;" |
 
  ! style="text-align: left;" |
 
{{Adsense 300x250}}
 
{{Adsense 300x250}}
−
 
−
{{Adsense linkblock 160x90}}
 
 
|}
 
|}
  
−
http://www.science-at-home.net/bilder/wikidata/mathematik/kreisring.gif
+
http://www.science-at-home.de/bilder/wikidata/mathematik/kreisring.gif
  
 
{|
 
{|
Zeile 168: Zeile 170:
 
|}
 
|}
  
−
http://www.science-at-home.net/bilder/wikidata/mathematik/kreisausschnitt.gif
+
http://www.science-at-home.de/bilder/wikidata/mathematik/kreisausschnitt.gif
  
 
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center"
 
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center"
Zeile 198: Zeile 200:
 
|<html><a href="http://www.amazon.de/gp/product/3860726382/ref=as_li_tf_il?ie=UTF8&camp=1638&creative=6742&creativeASIN=3860726382&linkCode=as2&tag=sciencehomede-21"><img border="0" src="http://ws-eu.amazon-adsystem.com/widgets/q?_encoding=UTF8&ASIN=3860726382&Format=_SL160_&ID=AsinImage&MarketPlace=DE&ServiceVersion=20070822&WS=1&tag=sciencehomede-21" ></a><img src="http://ir-de.amazon-adsystem.com/e/ir?t=sciencehomede-21&l=as2&o=3&a=3860726382" width="1" height="1" border="0" alt="" style="border:none !important; margin:0px !important;" /></html> || <html><a href="http://www.amazon.de/gp/product/382741797X/ref=as_li_tf_il?ie=UTF8&camp=1638&creative=6742&creativeASIN=382741797X&linkCode=as2&tag=sciencehomede-21"><img border="0" src="http://ws-eu.amazon-adsystem.com/widgets/q?_encoding=UTF8&ASIN=382741797X&Format=_SL160_&ID=AsinImage&MarketPlace=DE&ServiceVersion=20070822&WS=1&tag=sciencehomede-21" ></a><img src="http://ir-de.amazon-adsystem.com/e/ir?t=sciencehomede-21&l=as2&o=3&a=382741797X" width="1" height="1" border="0" alt="" style="border:none !important; margin:0px !important;" /></html>
 
|<html><a href="http://www.amazon.de/gp/product/3860726382/ref=as_li_tf_il?ie=UTF8&camp=1638&creative=6742&creativeASIN=3860726382&linkCode=as2&tag=sciencehomede-21"><img border="0" src="http://ws-eu.amazon-adsystem.com/widgets/q?_encoding=UTF8&ASIN=3860726382&Format=_SL160_&ID=AsinImage&MarketPlace=DE&ServiceVersion=20070822&WS=1&tag=sciencehomede-21" ></a><img src="http://ir-de.amazon-adsystem.com/e/ir?t=sciencehomede-21&l=as2&o=3&a=3860726382" width="1" height="1" border="0" alt="" style="border:none !important; margin:0px !important;" /></html> || <html><a href="http://www.amazon.de/gp/product/382741797X/ref=as_li_tf_il?ie=UTF8&camp=1638&creative=6742&creativeASIN=382741797X&linkCode=as2&tag=sciencehomede-21"><img border="0" src="http://ws-eu.amazon-adsystem.com/widgets/q?_encoding=UTF8&ASIN=382741797X&Format=_SL160_&ID=AsinImage&MarketPlace=DE&ServiceVersion=20070822&WS=1&tag=sciencehomede-21" ></a><img src="http://ir-de.amazon-adsystem.com/e/ir?t=sciencehomede-21&l=as2&o=3&a=382741797X" width="1" height="1" border="0" alt="" style="border:none !important; margin:0px !important;" /></html>
 
|-
 
|-
−
|<html><a href="http://www.amazon.de/gp/product/B00C3UV0QI/ref=as_li_tf_il?ie=UTF8&camp=1638&creative=6742&creativeASIN=B00C3UV0QI&linkCode=as2&tag=sciencehomede-21"><img border="0" src="http://ws-eu.amazon-adsystem.com/widgets/q?_encoding=UTF8&ASIN=B00C3UV0QI&Format=_SL160_&ID=AsinImage&MarketPlace=DE&ServiceVersion=20070822&WS=1&tag=sciencehomede-21" ></a><img src="http://ir-de.amazon-adsystem.com/e/ir?t=sciencehomede-21&l=as2&o=3&a=B00C3UV0QI" width="1" height="1" border="0" alt="" style="border:none !important; margin:0px !important;" /></html> || <html><a href="http://www.amazon.de/gp/product/3860726552/ref=as_li_tf_il?ie=UTF8&camp=1638&creative=6742&creativeASIN=3860726552&linkCode=as2&tag=sciencehomede-21"><img border="0" src="http://ws-eu.amazon-adsystem.com/widgets/q?_encoding=UTF8&ASIN=3860726552&Format=_SL160_&ID=AsinImage&MarketPlace=DE&ServiceVersion=20070822&WS=1&tag=sciencehomede-21" ></a><img src="http://ir-de.amazon-adsystem.com/e/ir?t=sciencehomede-21&l=as2&o=3&a=3860726552" width="1" height="1" border="0" alt="" style="border:none !important; margin:0px !important;" /></html>
+
|<html><a href="http://www.amazon.de/gp/product/3860726552/ref=as_li_tf_il?ie=UTF8&camp=1638&creative=6742&creativeASIN=3860726552&linkCode=as2&tag=sciencehomede-21"><img border="0" src="http://ws-eu.amazon-adsystem.com/widgets/q?_encoding=UTF8&ASIN=3860726552&Format=_SL160_&ID=AsinImage&MarketPlace=DE&ServiceVersion=20070822&WS=1&tag=sciencehomede-21" ></a><img src="http://ir-de.amazon-adsystem.com/e/ir?t=sciencehomede-21&l=as2&o=3&a=3860726552" width="1" height="1" border="0" alt="" style="border:none !important; margin:0px !important;" /></html> ||
 
|}
 
|}
  
−
http://www.science-at-home.net/bilder/wikidata/mathematik/kreisabschnitt.gif
+
http://www.science-at-home.de/bilder/wikidata/mathematik/kreisabschnitt.gif
  
 
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center"
 
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center"
Zeile 252: Zeile 254:
 
|}
 
|}
  
−
http://www.science-at-home.net/bilder/wikidata/mathematik/ellipse.gif
+
http://www.science-at-home.de/bilder/wikidata/mathematik/ellipse.gif
  
 
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center"
 
{| border="1" cellpadding="4" cellspacing="0" style="BORDER-COLLAPSE: collapse" borderColor="#336699" align="center"
Zeile 288: Zeile 290:
 
[[Kategorie:Mathematik]]
 
[[Kategorie:Mathematik]]
 
[[Kategorie:Geometrie]]
 
[[Kategorie:Geometrie]]
−
[[Kategorie:Formeln]]
+
[[Kategorie:Formel Geometrie]]
 
[[Kategorie:Ad man]]
 
[[Kategorie:Ad man]]
 
[[Kategorie:Ad man (amazon)]]
 
[[Kategorie:Ad man (amazon)]]

Version vom 25. März 2019, 13:48 Uhr

Kreis

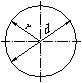
kreis.gif

A = (π · d²) / 4
d = √ ((A · 4) / π)


A = π · r²
r = √ (A / π)


U = π · d
d = U / π


U = 2π · r
r = U / 2π


Näherungswert/Faustformel für den Kreisumfang

U ≈ (22 / 7) · d 
A  Fläche
d  Durchmesser
r  Radius
U  Umfang
π  Kreiszahl Pi (≈ 3,14159)

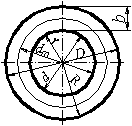
Kreisring

kreisring.gif

b = (D - d) / 2
D = d + b · 2
d = D - b · 2


dm = (D + d) / 2
D = dm · 2 - d
d = dm · 2 - D


A = (π / 4) · (D² - d²)
D = √ (d² + (A / π) · 4)
d = √ (D² - (A / π) · 4)


L = π · dm
dm = L / π 
A   Kreisringfläche
D   Außendurchmesser
d   Innendurchmesser
dm  mittlerer Durchmesser
R   Radius Kreisring außen
r   Radius Kreisring innen
b   breite des Kreisrings
L   gestreckte Länge
π   Kreiszahl Pi (≈ 3,14159)

Kreisausschnitt

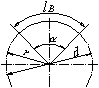
kreisausschnitt.gif

A = (π · d² · α) / (4 · 360°)


A = (r · lB) / 2


lB = (π · d · α) / 360° 
A   Fläche des Kreisausschnitts
d   Durchmesser
r   Radius
lB  Bogenlänge
α   Innenwinkel
π   Kreiszahl Pi (≈ 3,14159)

Kreisabschnitt

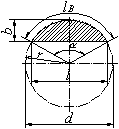
kreisabschnitt.gif

A = (lB · r - l (r - b)) / 2


A = (π · d² ) / 4 · (α / 360) - (l(r - b)/2)


A = (l · r - r² · sin (l/r)) / 2


A ≈ 2 / 3 · l · b
b ≈ (A · 3) / (2 · l)


lB = (π · r · α ) / 180° 
A   Fläche
r   Radius
d   Durchmesser
lB  Bogenlänge
l   Sehnenlänge
b   Breite
α   Innenwinkel

Ellipse

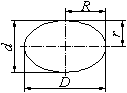
ellipse.gif

A ≈ (π · D · d) / 4


A = π · R · r


U ≈ π · (D + d) / 2


U ≈ π · (R + r) 
A  Fläche
d  kleine Achse
D  große Achse
r  kleine Halbachse
R  große Halbachse
U  Umfang


Pfad: Home / Mathematik / Geometrie / Kreis

Abgerufen von „http://www.science-at-home.de/wiki/index.php?title=Formeln_Kreis&oldid=36702“