Formeln Volumenkörper
Aus Wiki.sah
Würfel
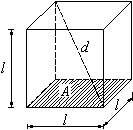
| V = A · l |
| V = l³ |
| A = l² |
| Ao = 6 · l² |
| d = l√3 |
V Volumen A Grundfläche l Kantenlänge Ao Oberfläche des Würfels d Raumdiagonale
Prisma
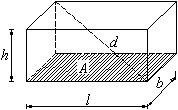
| V = A · h |
| V = l · b · h |
| d = √ (l² + h² + b²) |
| A = l · b |
| Ao = 2 (l · b + l · h + b · h) |
V Volumen A Grundfläche h Höhe b Breite l Länge Ao Oberfläche d Raumdiagonale
Zylinder
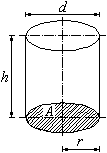
| V = A · h |
| V = π · r² · h |
| A = π · r² |
| A = (π · d²) / 4 |
| Ao = π · d · h + (π · d²) / 2 |
| h = (V · 4) / (π · d²) |
V Volumen A Grundfläche h Höhe d Durchmesser r Radius Ao Oberfläche
Kegel
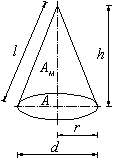
| V = (A · h) / 3 |
| V = π / 12 · d² · h |
| A = (π · d²) / 4 |
| AM = π · r · l |
| Ao = π · r (l + r) |
| Ao = AM + A |
| l = √(h² + r²) |
V Volumen A Grundfläche h Höhe d Durchmesser r Radius l Länge des Mantels AM Mantelfläche Ao Oberfläche
Kugel
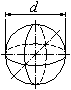
| V = (π · d³) / 6 |
| Ao = π · d² |
V Volumen d Durchmesser Ao Oberfläche
Pfad: Home / Mathematik / Geometrie / Volumenkörper